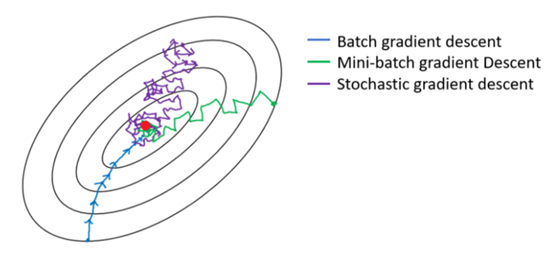
Batch gradient descent (batch size = N) takes relatively low noise, relatively large steps. And you could just keep matching to the minimum. However, it may take a long time to process and need additional memory.

Stochastic gradient descent (batch size = 1)  is easy to fit in memory and efficient for large datasets. But it can be extremely noisy since sometimes you hit in the wrong direction if that a training example happens to point in a bad direction. It won't ever converge, and will always just kind of oscillate and wander around the region of the minimum. 

in practice, mini-batch gradient descent with batch size in between 1 and N works better. It's not guaranteed to always head toward the minimum but it tends to head more consistently in direction of the minimum. 

University of Michigan - Ann Arbor

Batch Gradient Descent requires the entire dataset to be processed to complete one step. Gradient Descent can require many steps in some cases which causes this procedure to be very slow and inefficient for large datasets.

Mini-Batch Gradient Descent solves this problem by taking small groups of random data points called mini-batches and using them to estimate each step.  The mini-batches are usually a size greater than 1 but less than N (dataset size). The smaller steps allow for a much faster algorithm.

Mini-Batch Gradient Descent

Assuming that the error function is $J(w)$ with one parameter $w$, to minimize the error, we can update the weight $w$ as follows.
$$w = w - \alpha * \frac{dJ(w)}{dw}$$
, where $\alpha$ is a learning rate, and $\frac{dJ(w)}{dw}$ is the derivative of $J(w)$ with respect to $w$.

If the error function has two or more parameters, for example, a weight $w$ and a bias $b$, we can update them one by one.
$$w = w - \alpha * \frac{\partial J(w,b)}{\partial w}$$
$$b = b - \alpha * \frac{\partial J(w,b)}{\partial b}$$
, where $\partial$ is a stylish cursive $d$, denoting the partial derivatives.

(Batch) Gradient Descent (Deep Learning Optimization Algorithm)

If we choose the mini-batch size to be 1, then it gives the algorithm called Stochastic Gradient Descent or SGD.

In this case, on every iteration, you're taking gradient descent with just a single training example
$w = w - \alpha \nabla_w J(x^i, y^i; w)$

The most important property of SGD is that computation time per step does not grow with the number of examples. This makes SGD very efficient with large training sets.

The learning rate is a hyperparameter that must be adjusted. Unlike regular parameters of a model (weights like w and b), which are learned by the algorithm from the training set, hyperparameters are special parameters chosen by the algorithm designer that affect how the algorithm works.

Stochastic Gradient Descent Algorithm

Machine Learning Yearning, a free ebook from Andrew Ng, teaches you how to structure Machine Learning projects.
https://www.deeplearning.ai/machine-learning-yearning/

Note: The content of the book is aligned with the Coursera Deeplearning.ai specialization.  https://www.deeplearning.ai/deep-learning-specialization/ 

Machine Learning Yearning (Deeplearning.ai)

A helpful website for understanding gradient descent:
https://towardsdatascience.com/gradient-descent-explained-9b953fc0d2c

Gradient Descent Reference

If you have a huge training set with 5000000 training samples,
$X=[ x^{(1)},  x^{(2)}  ,...,  x^{(5000000)}]$
Let's say each of your baby training sets have just 1,000 examples each. So, you take the first mini-batch as $X^{\{ 1\}} =[x^{(1)},  x^{(2)}  ,...,  x^{(1000)}] $. And then you take home the next 1,000 samples $X^{\{2\}} =[x^{(1001)},  ...,  x^{(2000)}] $ and so on.

Altogether you would have 5,000 of these mini-batches and then similarly you do the same thing for Y. Hence we end up with mini-batches $X^{\{ T\}}, Y^{\{ T\}}$, T = 1,2...,5000.

An Example of Mini-Batches

for t = 1, 2,...N: (N is the number of mini-batches)
 - Forward propagate on $X^{\{ t\}}$
 - Compute cost function $J^{\{ t\}}$
 - Backpropagate to compute gradients wrt $J^{\{ t\}}$ (using $X^{\{ t\}}$,$Y^{\{ t\}}$)
 - $W^{[l]} =W^{[l]}-\alpha dW^{[l]}, b^{[l]} = b^{[l]}-\alpha db^{[l]}$

This is one pass through your training set using mini-batch gradient descent. It is also called doing one epoch of training.

Mini-Batch Gradient Descent Algorithm

Batch vs Stochastic vs Mini-Batch Gradient Descent

First, we take a constant learning rate represented by the blue line. We see that, as we iterate, the steps are large and noisy and do not converge on a minimum. Instead, it wanders around the minimum.

Next, we take a decaying learning rate represented by the green line. At the start, the learning rate takes large steps with each iteration. But the learning rate is reduced or decayed as it approaches the minimum. This slower learning rate takes smaller tighter steps around the minimum and is closer to convergence.

This method allows us to have relatively fast learning during the initial phases with large steps, but also converge to a minimum during the final phases with slower learning rates and smaller steps.

Example Using Mini-Batch Gradient Descent (Learning Rate Decay)

If your training set is small (m < 2,000), it's better to use Batch Gradient Descent.
Make sure that every mini-batch fits in your CPU/GPU memory.
It is a common practice to use powers of two as a mini-batch size: 64, 128, 256. This is related to the fact that the number of physical processors of the GPU tend to be a power of 2.
If the batch size is too small, the loss curve will oscillate and affect the stability of training

Mini-Batches Size

Which of these statements about mini-batch gradient descent do you agree with?

Why is the best mini-batch size usually not 1 and not m, but instead something in-between?

Which of the following do you agree with?

Suppose your learning algorithm’s cost J, plotted as a function of the number of iterations, looks like the image below:

If we only have two features, $x_1$ and $x_2$, in order to minimize the loss function, we can apply gradient descent to update $w_1$, $w_2$, and $b$.
To compute the derivatives of $\mathcal L (a, y)$ with respect to $w_1$, $w_2$, and $b$, we need to compute the derivatives of $\mathcal L (a, y)$ with respect to $a$ and $z$ first.
$$\mathcal L (a, y) = -(ylog(a) + (1 - y)log(1 - a)) \Rightarrow$$
$$\frac{d\mathcal L (a, y)}{da} = -\frac{y}{a}+\frac{1-y}{1-a}$$
$$a = \sigma(z) = \frac{1}{1 + e^{-z}} \Rightarrow \frac{da}{dz} = a(1-a) \Rightarrow$$
$$\begin{aligned}
\frac{d\mathcal L (a, y)}{dz} & = \frac{d\mathcal L (a, y)}{da}\frac{da}{dz} \\
& = (-\frac{y}{a}+\frac{1-y}{1-a})*(a(1-a)) = a-y \\
\end{aligned}$$
$$\begin{aligned}
\frac{d\mathcal L (a, y)}{dw_1} & = \frac{d\mathcal L (a, y)}{dz}\frac{dz}{dw_1} = (a-y)*x_1 \\ 
\end{aligned}$$
$$\begin{aligned}
\frac{d\mathcal L (a, y)}{dw_2} & = \frac{d\mathcal L (a, y)}{dz}\frac{dz}{dw_2} = (a-y)*x_2 \\ 
\end{aligned}$$
$$\begin{aligned}
\frac{d\mathcal L (a, y)}{db} & = \frac{d\mathcal L (a, y)}{dz}\frac{dz}{db} = (a-y)*1 = (a-y)
\end{aligned}$$

Logistic regression gradient descent

The gradient $\nabla_x f(x)$ of a scalar function $f(x_1, x_2, x_3, ..., x_n)$ is defined as the unique vector field whose dot product with any vector $v$ at each point $x$ is the directional derivative of $f$ along $v$. That is,
$ \nabla_x f(x) \cdot  v = \nabla_v f(x) $

The directional derivative in direction $v$ (a unit vector) is the slope of the function $f$ in direction $v$, namely the rate of increase of $f$ per unit of distance moved in the direction given by $v$. 

To minimize $f$, we would like to ﬁnd the direction in which $f$ decreases the fastest. We can do this using the directional derivative:
$\min_{v, v^Tv = 1} \nabla_x f(x) \cdot  v= \min_{v, v^Tv = 1} ||\nabla_x f(x)||_2 ||v||_2 \cos \theta$
where θ is the angle between $v$ and the gradient. Substituting in $||v||_2= 1$ and ignoring factors that do not depend on $v$, this simpliﬁes to $\min_{v}cos θ$.

This is minimized when $v$ points in the opposite direction as the gradient. In otherwords, the gradient points directly uphill, and the negative gradient points directly down hill. We can decrease $f$ by moving in the direction of the negative gradient.

Hence we have $x' = x-\alpha \frac{df(x)}{dx}$ where $\alpha$ is the learning rate, a positive scalar determining the size of the step.

Derivation of the Gradient Descent Formula

Epoch is every iteration of gradient descent through the entire training set.

Epoch in Gradient Descent

The basic idea of gradient descent with momentum is to compute an exponentially weighted average of your gradients, and then use that gradient to update your weights instead. It almost always works faster than the standard gradient descent algorithm.


Gradient Descent with Momentum

For logistic regression, the gradient is given by ∂∂θjJ(θ)=1m∑mi=1(hθ(x(i))−y(i))x(i)j. Which of these is a correct gradient descent update for logistic regression with a learning rate of α?

Does adding polynomial features (e.g., instead using $h\theta(x)=g(\theta0+\theta1x1+\theta2x2+\theta3x21+\theta4x1x2+\theta5x22) )$ could increase how well we can fit the training data?

Suppose you have the following training set, and fit a logistic regression classifier $h\theta(x)=g(\theta0+\theta1x1+\theta2x2)$.

The objective of backpropagation is to change the weights for the neurons, in order to bring the error function to a minimum with the help of gradient descent. 

Backpropagation calculates how much the final output values are affected by each of the weights. To do this, it calculates partial derivatives, going back from the error function to the neuron that carried a specific weight.

Backward Propagation

- Adam is fast, but tends to overfit
- SGD is slow but gives great results
- RMSProp sometimes works best
- SWA can easily improve quality
- AdaTune magically improves the learning rate

Learn Before

Related